Keplerian Elements
Understanding the motion of planets and satellites can seem complex, but the Six Keplerian Elements make it easier to describe satellite orbits with high precision. Named after the astronomer Johannes Kepler, these six parameters provide a framework for defining an orbit mathematically. Whether we’re discussing a planet orbiting the sun or an artificial satellite circling the Earth, these elements are essential in understanding orbital motion. Let’s break them down, step by step, from simple to more technical, using everyday examples to help clarify each one.
The Six Keplerian Elements:
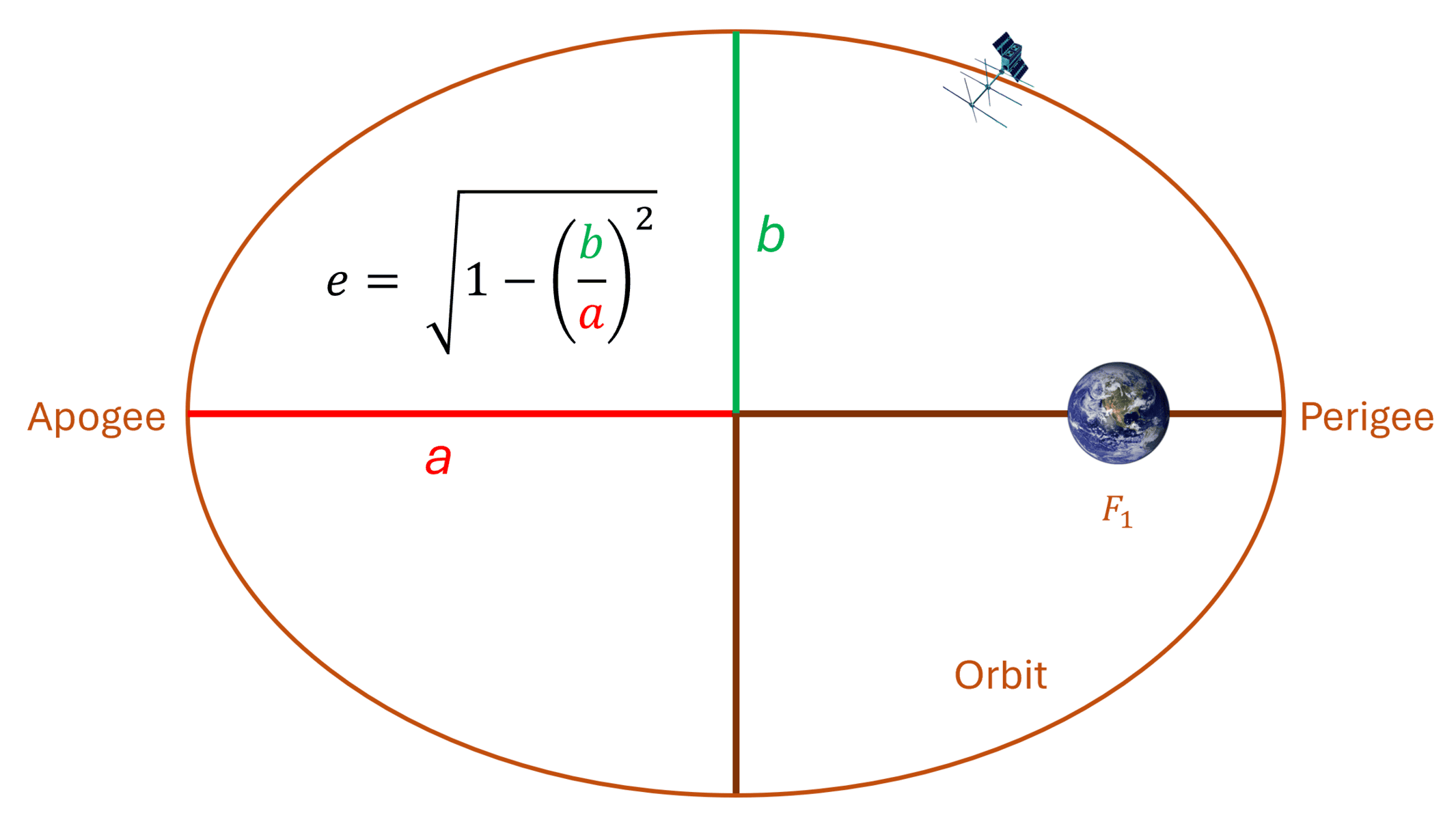
1. Semi-major Axis (a):
The semi-major axis represents the orbit’s size, which is half the length of the elliptical path’s longest diameter (equal to the radius, if the orbit is a perfect circle). Think of it like a racetrack: if you increase the size of the track, it takes longer to complete a lap. In orbital terms, this axis determines how long it takes for an object to make one complete orbit. The bigger the orbit, the longer the period. It’s a critical factor in understanding both natural and artificial objects in orbit.
2. Eccentricity (e):
Eccentricity describes how much the orbit deviates from being a perfect circle. An eccentricity of 0 means the orbit is circular, while an eccentricity closer to 1 indicates an elongated ellipse. Picture the orbit as a rubber band: a perfectly circular orbit would be like a fully relaxed rubber band, while a more eccentric orbit would be like one stretched into an oval shape. This element plays a major role in understanding how close or far an object will get from the center of attraction during its orbit.

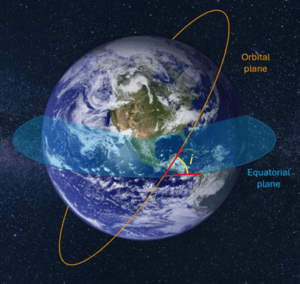
3. Inclination (i):
Inclination refers to the tilt of the orbit’s plane relative to a reference plane—typically the equatorial plane of the planet it orbits. Imagine tilting a plate slightly; the greater the inclination, the steeper the tilt of the orbital plane. Inclination is measured in degrees, and it’s crucial for defining whether an object orbits near the equator, at the poles, or somewhere in between. A 0° inclination means the object moves along the equator, while a 90° inclination means it travels over the poles.
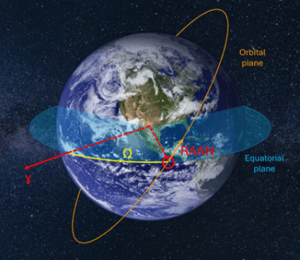
4. Longitude of the Ascending Node (Ω):
This parameter describes the orientation of the orbit’s plane horizontally. To picture this, imagine you’re walking up a spiral staircase: the “ascending node” is the point where you step from one floor to the next. In orbital mechanics, it refers to where the object crosses the equatorial plane, moving from the southern hemisphere to the northern hemisphere. The longitude of the ascending node specifies the angle between a reference direction (such as the position of the vernal equinox) and this crossing point.
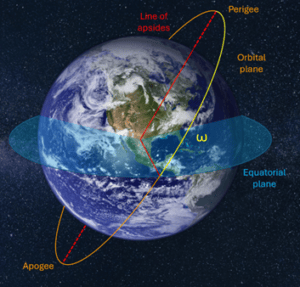
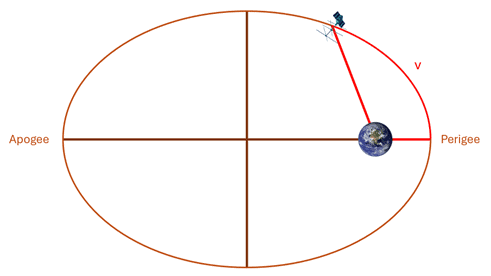
5. Argument of Perigee (ω):
This parameter defines the orbit’s orientation within its plane. Specifically, it measures the angle between the ascending node and the point where the object comes closest to the planet, called the perigee. Think of it like plotting the closest point on an elliptical track where a runner might pass the spectator stands. Knowing the argument of perigee is essential for understanding when an object will be nearest to its central body.
University of Bristol has made an animated visualization of the 6 Keplerian Elements here
6. True Anomaly (ν):
True anomaly indicates the object’s current position in its orbit at a given time, expressed as the angle between the perigee (the closest approach to the central body) and the object’s actual location. For a real-world analogy, think of it as keeping track of a runner’s progress along a circular track: you can measure how far along they are from a specific starting point, which in orbital terms is the perigee. True anomaly is especially useful for determining the exact position of a satellite or planet at any given moment.
TLE
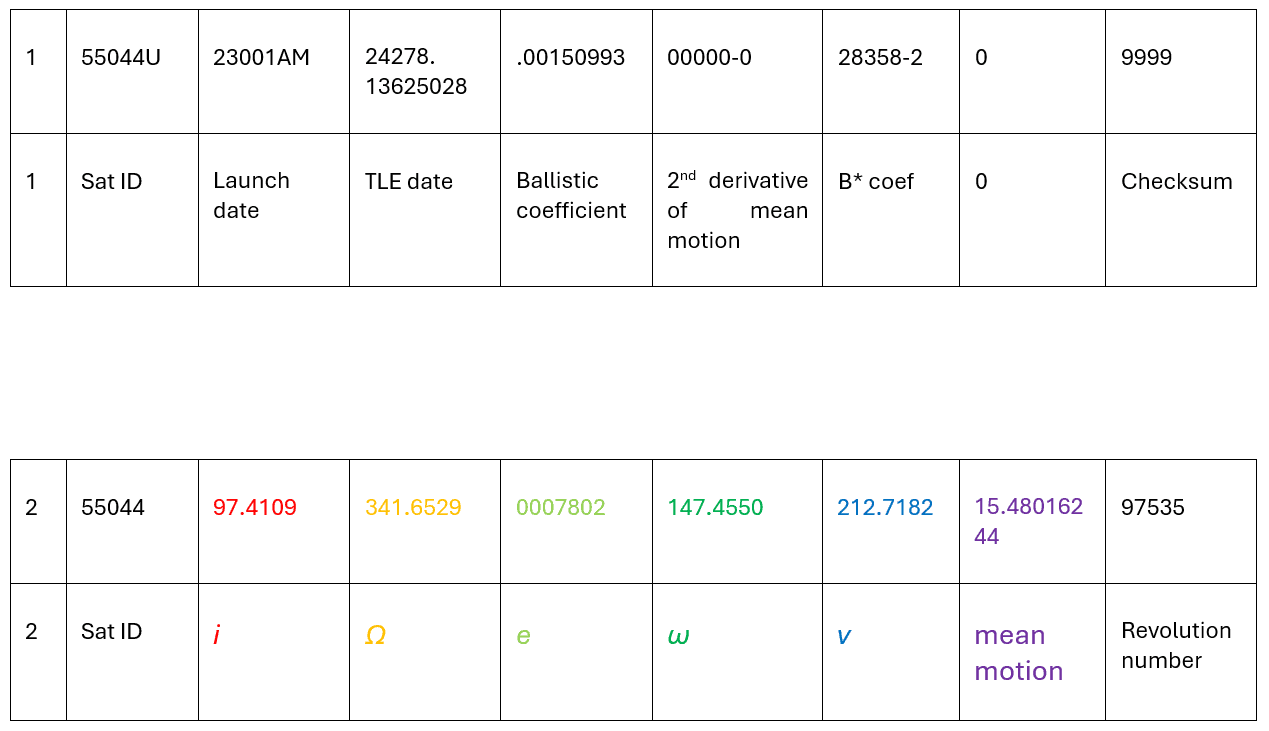
One can find the Keplerian elements, except for the semi-major axis (a) in the Two-Line Element (TLE) of a space object. This element is a set of different values that correspond to the position of the satellite, its identification number, date of launch, and other physical characteristics.
5 of the 6 Keplerian elements can be read directly from that TLE. To recover the semi-major axis (a) of the spacecraft, we need to look at the mean motion of the satellite: the number of revolutions around the heavenly body that the satellite completes every mean solar day (24 hours). Based off this, one can calculate the orbital period of the satellite, then from the laws of Kepler, find the corresponding semi-major axis.
The TLE beholds all the information one needs to find the position of a satellite at a given moment. The additional information allows for propagation. Using various propagating models, one can estimate the future positions of the satellite thanks to the TLE.
1 55044U 23001AM 24278. 13625028 .00150993 00000-0 28358-2 0 9999
2 55044 97.4109 341.6529 0007802 147.4550 212.7182 15.48016244 97535
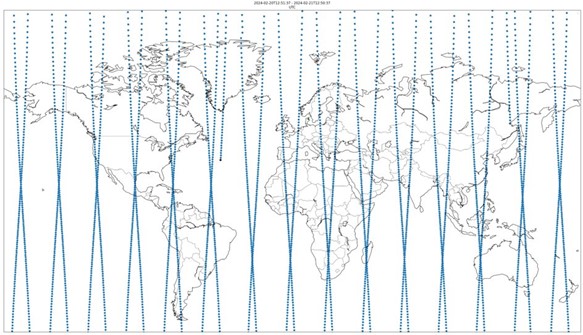
Visualizing Orbits through Ground Tracks
To help visualize how these elements come together, we can observe the ground tracks of satellites over time. Ground tracks show the path a satellite appears to trace over the Earth’s surface as it orbits, influenced by its inclination, semi-major axis, and eccentricity. For example, with an inclination near 0°, a satellite’s ground track would closely follow the equator. But with a higher inclination, the track sweeps north and south, appearing to weave across the globe. Over 24 hours, this trace gives us a complete picture of where the satellite passes overhead, based on its orbital characteristics.
These Six Keplerian Elements provide a comprehensive framework for understanding orbital mechanics. Whether describing the motion of natural celestial bodies or satellites, they are critical for modeling the dynamics of objects in space. From simple shapes like circles and ellipses to more detailed factors like orbital tilt and specific positions along the path, these elements allow us to predict and track the movement of objects with remarkable precision.
Published on 25/10/2024, Written by: Cyriaque Guillot, Mathias Mose Gjelstrup, Ivan Conti



